Dynamic Programming, Recursion and Memoization | LCS Problem

This article works around the relation of Dynamic Programming, Recursion and Memoization. It explores the three terms separately and then shows the working of these together by solving the Longest Common Subsequence Problem effectively.

Recursion

Recursion is a method of solving a problem where the solution depends on the solution of the subproblem.

In  simple words, Recursion is a technique to solve a problem when it is much easier to solve a small version of the problem and there is a relationship/hierarchy between the different versions/level of problem. 

Recursion is very similar to the concept of induction (which is a mathematical proof technique) which is the procedure to prove an equation with 2 simple steps-

1. Base Case- Compute the equation with input=1 and see, if the output matches the desired output.
2. Induction Step- Compute the equation with input=k+1, assuming the input=k has given us the desired output. If the equation with input=k+1, holds true, then we have proven the equation.

Now let us understand how induction works which will lay the foundation for understanding recursion.

1. It works on the basic principle that when we prove a relation that the equation with n+1 holds true, if it is true for n. Then similarly, the same relation can be proved for n and n-1 and so, on till n becomes 2 and n-1 becomes 1.
2. The above relation needs a base case(which is basically the solution of an easy subproblem) and for induction it is always an equation with n=1.

So, now when we know an equation is true for n=1, we can use the bottom-up approach and reach till n(which is the whole problem). 

The concept of recursion is very similar to that of induction with only difference being that our base case does not have to be n=1 and the induction step need not be adjacent nos. In case of recursion, we can have a generic base case and an induction step.

Let us see an example and understand the base case and induction step philosophy which drives recursion and makes it a very popular approach for problems which can be divided into smaller sections and have relation between these vertical levels.

Question:-

Find Factorial of a number.

Formula:- n! = 1*2*3*…….*n

Approach:- 

If we see the formula we can see that factorial of n has a relation with factorial of n-1 and so on.

In other words, n! = n* (n-1)!

We can have a recursive formula to keep on multiplying the given number (n) with a factorial of the next small number(n-1) (induction step) till we reach 1 because we know 1! = 1 (base case).

Solution:-

public class Factorial {
    public static void main(String[] args) {
        int number = 6;
        long factorial = findFactorial(number);
        System.out.println("Factorial of " + number + " = " + factorial);
    }
  
    public static long findFactorial(int number)
    {
      if (number == 1) {
        return 1;
      }
      
      return number * findFactorial(number - 1);
    }
}

Memoization

According to Wikipedia, In computing, memoization or memoisation is an optimisation technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again.

In simple words, Memoization is used for problems that need to execute a function with the same set of arguments multiple times and the computation takes a lot of time hence, caching/storing the result saves a lot of computation time.

Let us understand the concept of memoization better through an example:-

Question:- Find the Nth term of a fibonacci series.

Formula:- fib(n) = fib(n-1) + fib(n-2) where fib(0)=1 and fib(1a)=1

Approach:- By the looks of the problem statement and formula, it seems like a very simple recursive solution.

Basically, we have to recursively traverse to the n-1 and n-2 function(induction step) till we reach n=1 or n=0 as we know their values.

Now, let us see the solution of this approach by a flow diagram.

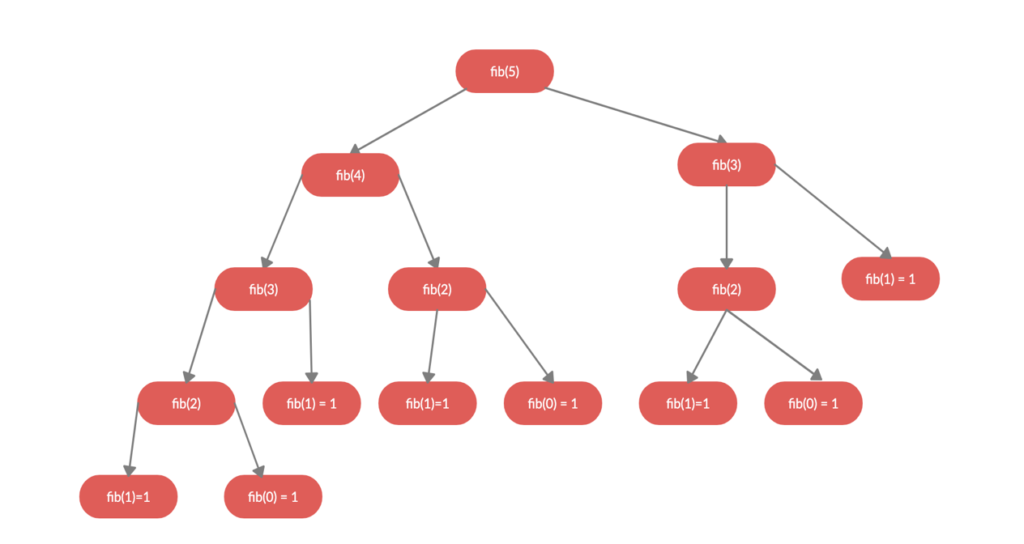
Now, if we see the above flow chart, we can easily see the issue that multiple nth term is getting computed again and again and with this approach,

Time Complexity:- O(2*n)

Space Complexity:- O(1) (here, we are not considering the recursion related stack space)

From the above example, we can also see, for each value the underneath flow chart is always the same i.e the solution/answer will always be the same. Hence, if we cache them we can drastically reduce the time complexity.

Solution:-

public class Fibonacci {
    public static void main(String[] args) {
        int number = 5;
        int[] memoizedAns = new int[6];
      
        //base case
        memoizedAns[0] = 1;
        memoizedAns[1] = 1;
      
        long fibonacci = findFibonacci(number, memoizedAns);
        System.out.println(number + "th number of fibonacci series = " + fibonacci);
    }
  
    public static long findFibonacci(int number, int[] memoizedAns)
    {
      if (memoizedAns[number] != 0) {
          //value for number has been already computer, hence using the memoized value.
          return memoizedAns[number];
      }
      
      //caching the computing values
      memoizedAns[number] =  findFibonacci(number-1, memoizedAns) + findFibonacci(number-2, memoizedAns);
      return memoizedAns[number];
    }
}

As, we can see in the solution, while computing values that are not already cached, we cache the computed value after computing values. Hence, for finding nth number in fibonacci series, we will always compute the 1 to nth number only once and hence,

Time Complexity:- O(n)

Space Complexity:- O(n) (here, we are not considering the recursion related stack space)

Dynamic Programming

Dynamic programming is a technique to solve a complex problem by dividing it into subproblems. This technique should be used when the problem statement has 2 properties:

1. Overlapping Subproblems- The term overlapping subproblems means that a subproblem might occur multiple times during the computation of the main problem.
   For example- In the above fibonacci series problem, we saw that many subproblems occurred multiple times while solving the main problem.
   
   There are 2 ways to optimise the overlapping problem-
   1. Memoization (Top-Down Approach)
   2. Tabulation (Bottom-Up Approach)
   
2. Optimal Substructure- A problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems.

Longest Common Subsequence

Question:- Given two sequences, find the length of longest subsequence present in both of them.

For example-

LCS of “ABCDEF” and “BDF” is “BDF” of length 3.

Approach:-

Assume 2 string s1 and s2 of length n and m respectively.

Let us start from the last character(l1 and l2) of each string and let us check whether it can be a part of the longest substring or not:-

1. l1 and l2 match, so that means that they can be a part of the longest substring.
   
   LCS(s1, s2, n, m) = 1 + LCS(s1, s2, n-1, m-1) (induction step)
2. l1 and l2 do not match, which means that either l1 or l2 cannot be part of the longest sequence.
   
   LCS(s1, s2, n, m) = max(LCS(s1, s2, n-1, m), LCS(s1, s2, n, m-1)) (induction step)

And we can continue traversing down, till we reach n=0||m=0 in which case the longest subsequence will be 0(base case).

Below is the flowchart of the given pseudo code.

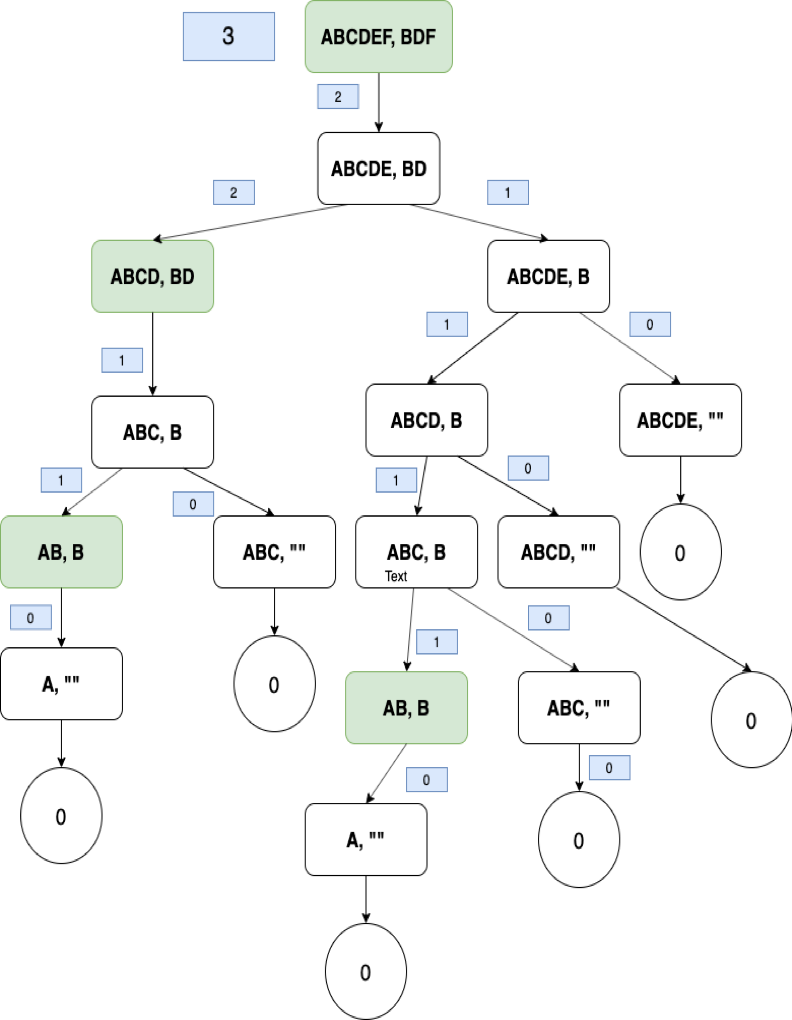
As you can see, through basic recursion, we come across overlapping subproblems and we can also view that the optimal structure of the problem is computed through the optimal structure of the subproblem. 

Time Complexity:- O(2*(mn))

Space Complexity:- O(1)

Now, at this point Dynamic Programming comes into picture.

Solution:-

public class LCS {
  public static void main(String[] args) {
    String s1 = "ABCDEF";
    String s2 = "BDF";
    int n = s1.length();
    int m = s2.length();
    int[][] ans = new int[n][m];
    for (int[] e : ans) {
      Arrays.fill(e, -1);
    }
    System.out.println("Length of the Longest Subsequence is" + findLCS(s1, s2, n-1, m-1, ans));
  }
  
  public static long findLCS(String s1, String s2, int n, int m, int[][] ans) {
    if (n<0 || m<0) {
      return 0;
    }
    
    if(ans[n][m]!=-1) {
      return ans[n][m];
    }
    
    if(n==0 || m==0) {
      ans[n][m] = 0;
      return ans[n][m];
    }
    
    if(s1.charAt(n)==s2.charAt(m)) {
      ans[n][m] = 1 + findLCS(s1, s2, n-1, m-1, ans);
    } else {
      ans[n][m] = Math.max(findLCS(s1, s2, n-1, m, ans), findLCS(s1, s2, n, m-1, ans));
    }
    
    return ans[n][m];
  }
}

As we can see, from the above solution memoization, recursion and dynamic programming work hand in hand in optimising the solution.

Time Complexity:- O(mn)

Space Complexity:- O(mn)

Conclusion

That’s all from my side. For more understanding on how Recursion, Memoization and Dynamic Programming go hand in hand, kindly study regarding some more famous Dynamic Programming problem statements like:-

1. Longest common subsequence problem
2. Longest palindromic substring
3. All-Pairs Shortest Path

Thanks for reading.